Feed Forward Propagation from Andrew Ng Machine Learning Lecture

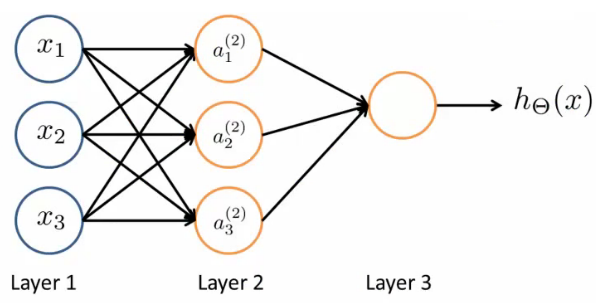
Neural networks are a series of stacked layers. Deeper the network, higher the number of layers. Layer 1 is called the input layer and Layer 3 is called the Output layer. The intermediate layer are called the hidden layer. The number of hidden layer might vary depending on the network complexity. In this case, Layer 2 is the hidden layer. \(x = \begin{bmatrix} x1 \\ x2 \\ x3 \\ \end{bmatrix}\)

\[\theta = \begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \\ \end{bmatrix}\]

\(a = g( \theta^T * x ) \\\) g is the activation function . x is the input vector . a is the activation output.

\[a^{(2)}_1 = g( \theta^{(1)}_{10} x_0 + \theta^{(1)}_{11} x_1 + \theta^{(1)}_{12} x_2 + \theta^{(1)}_{13} x_3)\] \[a^{(2)}_2 = g( \theta^{(1)}_{20} x_0 + \theta^{(1)}_{21} x_1 + \theta^{(1)}_{22} x_2 + \theta^{(1)}_{23} x_3)\] \[a^{(2)}_3 = g( \theta^{(1)}_{30} x_0 + \theta^{(1)}_{31} x_1 + \theta^{(1)}_{32} x_2 + \theta^{(1)}_{33} x_3)\]

Dimension of weight matrix

S be the units in Layer 1 .

S = 3 ( Discarding Bias Unit )

T be the units in Layer 2.

T = 3 ( Discarding the Bias activation Unit )

The Dimension is given by ( S * T+1 ).

The Dimension of weight matrix is 3 * 4

\(\begin{bmatrix} \theta^{(1)}_{10} & \theta^{(1)}_{11} & \theta^{(1)}_{12} & \theta^{(1)}_{13} \\ \theta^{(1)}_{20} & \theta^{(1)}_{21} & \theta^{(1)}_{22} & \theta^{(1)}_{23} \\ \theta^{(1)}_{30} & \theta^{(1)}_{31} & \theta^{(1)}_{32} & \theta^{(1)}_{33} \\ \end{bmatrix}\)

\[\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ \end{bmatrix} = \sigma \begin{pmatrix} \begin{bmatrix} \theta^{(1)}_{10} & \theta^{(1)}_{11} & \theta^{(1)}_{12} & \theta^{(1)}_{13} \\ \theta^{(1)}_{20} & \theta^{(1)}_{21} & \theta^{(1)}_{22} & \theta^{(1)}_{23} \\ \theta^{(1)}_{30} & \theta^{(1)}_{31} & \theta^{(1)}_{32} & \theta^{(1)}_{33} \\ \end{bmatrix} * \begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ \end{bmatrix} + \begin{bmatrix} b_o \\ b_1 \\ \vdots \\ \end{bmatrix} \end{pmatrix}\]

The hypothesis function is given by,

\[h_{\theta}(x) = g( \theta_{10}^{(2)} a_{(0)}^{(2)} + \theta_{11}^{(2)} a_{(1)}^{(2)} + \theta_{12}^{(2)} a_{(2)}^{(2)} + \theta_{13}^{(2)} a_{(3)}^{(2)} )\]

We replace

\[z^{(2)}_1 = \theta^{(1)}_{10} x_0 + \theta^{(1)}_{11} x_1 + \theta^{(1)}_{12} x_2 + \theta^{(1)}_{13} x_3\]

The final Equation,

\[a_1^{(2)} = g(z_1^{(2)})\] \[a_2^{(2)} = g(z_2^{(2)})\] \[a_3^{(2)} = g(z_3^{(2)})\] Written on September 27th, 2018 by Karthik