Complete IoU

The loss functions are the major driving force in training a good model. In Object detection and Instance segmentation tasks, the most widely used loss function is Intersection over Union (IOU). In Enhancing Geometric Factors for Object Detection and Instance Segmentation Loss function. paper, a new loss function called as Complete Intersection over Union is proposed by considering three geometric factors.

Before that, Let’s understand Intersection over Union

Intersection over Union

Intersection over Union is the ratio of Area of Overlap over Area of Union. In the below figure, B is the ground truth box and A is the predicted bounding Box.

\[IOU = \frac{|A \cap B|}{|A \cup B}\]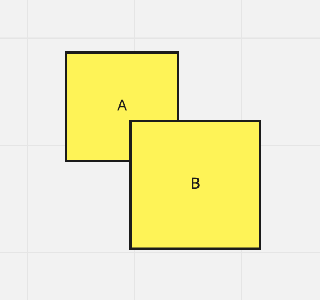

How does IoU loss help in detection or segmentation model training?

It is the ratio of predicted bounding box overlapping over the ground truth area box. There are two extreme scenarios here. The positive scenario, where both the box overlap 100%, then the IoU ratio will be 1. On the other hand, the negative scenario, when the predicted box is far away from the ground truth box without any overlap, then the IoU value will be 0. By taking (1 - IoU) the loss will become maximum. The performance of the model must be improved by reducing this loss.

IoU has scale invariance property. This means, the width, height and location of the two bounding boxes are taken into consideration. The normalized IoU measure focuses on the area of the shapes, no matter their size.

The problem to distinguish between the same level of overlap, but different scales will give different values. State of the art object detection networks deal with this problem by introducing ideas such as anchor boxes and non-linear representations.

Generalized Intersection over Union

\[GIoU = \frac{|A \cap B|}{|A \cup B} - \frac{C\setminus( A \cup B)}{|C|} \ = IoU - \frac{C\setminus( A \cup B)}{|C|}\]

Here, A and B are the prediction and ground truth bounding boxes. C is the smallest convex hull that encloses both A and B. C is the smallest box covering A and B.

The penality term in GIoU loss, will move the predicted box towards the target box in non-overlapping cases.

In this paper, a new CIoU loss is introduced by considering the geometric factors in bounding box regression. This loss as improved the average precision and average recall without the sacrifice of inference efficiency.

Comparision of GIoU and CIoU

GIoU loss tries to maximize overlap area of two boxes and still performs limited due to only considering overlap areas.

GIoU loss tends to increase the size of the predicted box, while the predicted box moves towards the target box very slowly. Consequently , GIoU loss emprically needs more iterations to converge, especially for bounding box at horizontal and vertical orientations, thus increasing the training time.

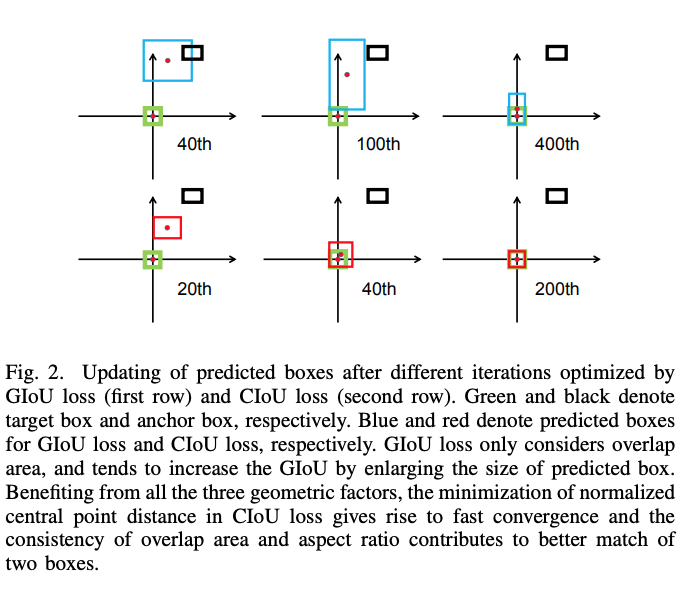
CIoU depend on three geometric factors for modelling regression relationships.

\[CIoU = S (A, B) + D(A, B) + V(A, B) \\\]

S - Overlap Area
D - Normalized central point distance
V - Aspect Ratio

These three geometric factors are incorporated into CIoU loss for better distinguishing difficult regression cases.

For detection tasks, generally (Ln-norm) Mean squared Error loss and Smooth loss is been widely used for object detection, pedestrian detection, pose estimation and instance segmentation. However, recent works suggest that Ln-norm based loss functions are not consistent with the evaluation metric, instead propose Intersection over Union.

Overlap Area

The previous IoU and GIoU loss has proven overlap area calculation. Hence the overlap area employs the same IoU loss. \(S = 1 - IoU\)

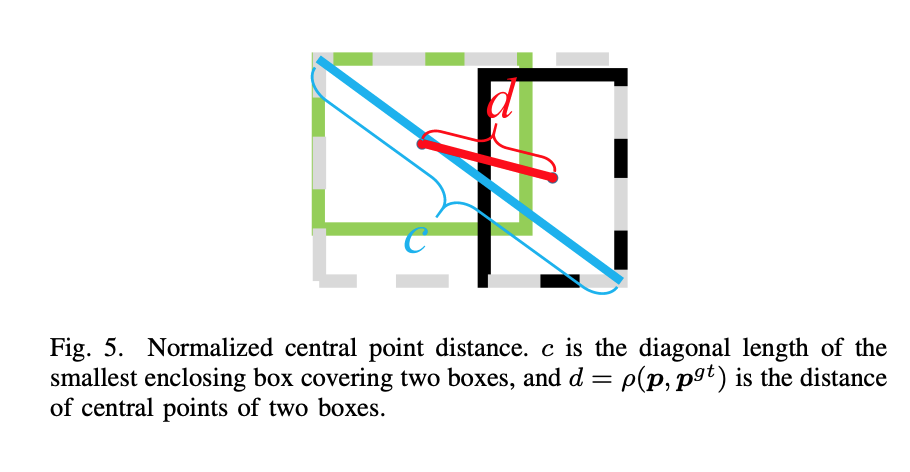
Normalized central point distance

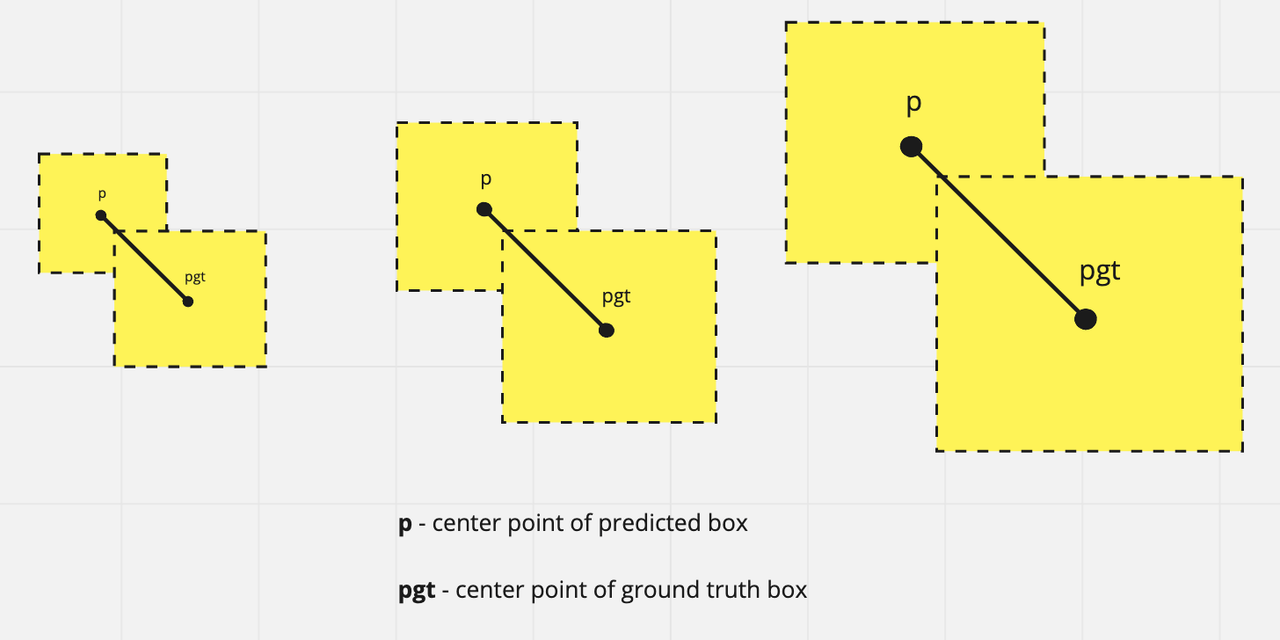
In the above overlapping scenarios, the distance might vary across different training observations. To solve this, the distance is normalized.

Both Normalized central point distance and Aspect ratio must be invariant to regression scale, Hence the normalized central point distance to measure the distance of two boxes is employed.

\[D = \frac{(Euclidean \ distance \ ( A, B))^2}{c^2}\]

Aspect ratio

\[V = \alpha \ (\frac{4}{\pi^2}(arctan(\frac{w^B}{h^B}) - arctan(\frac{w}{h}))^2) \\ w^B \ width \ of \ ground \ truth \ box \\ h^B \ height \ of \ ground \ truth \ box\]

\[\alpha = 0, \\if \ IoU < 0.5\]

\[\alpha = \frac{V}{(1-IoU) + V} \\ if \ IoU \ge 0.5\]

alpha is a trade-off parameter. When the IoU is less than 0.5, then the two boxes are not well matched, the consistency of aspect ratio is less important.

CIoU loss can provide moving direction for bounding boxes when non-overlapping with target box.

Loss Visualization

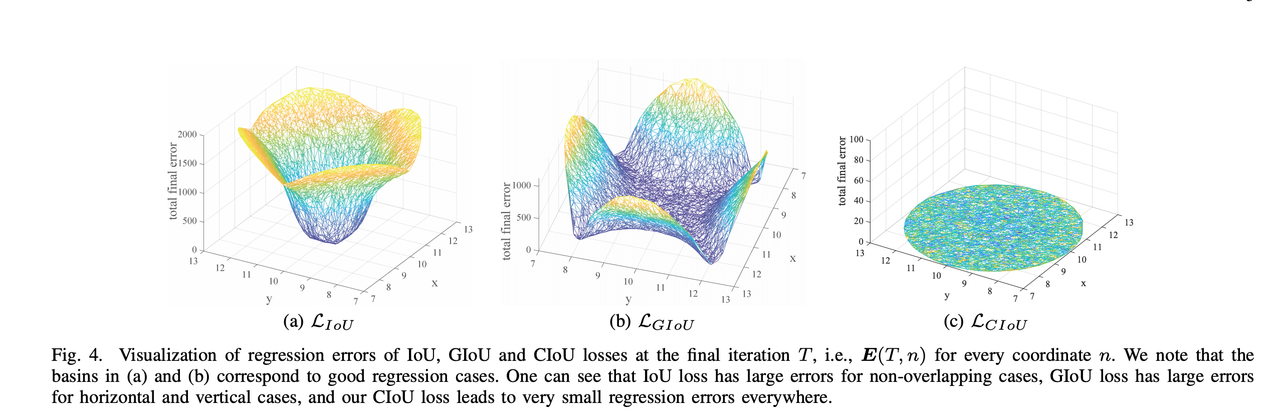
CIoU loss improves the performance of detection and segmentation tasks. CIoU converges faster with less iterations than IoU and GIoU due to the consideration of three geometric factors.

Resources

https://giou.stanford.edu/

Written on May 9th, 2020 by Karthik

Feel free to share!